• Задания 1-10
• Задания 11-13
• Задание 14 и 15

Навигация по странице:

• Задание 1
• Задание 2
• Задание 3
• Задание 4
• Задание 5
• Задание 6
• Задание 7
• Задание 8
• Задание 9
• Задание 10

 

Задание 1.Умение оценивать количественные параметры информационных объектов.

Справка

Количество символов в алфавите (мощность алфавита) находится по формуле N=2^I, где I – информационный вес одного символа (в битах).

Информационный объем сообщения (текста) определяется по формуле  I = К·i, где К - количество символов в сообщении (тексте), I – информационный вес одного символа (в битах)

Пример заданий:

1) Информационное сообщение объемом 450 бит состоит из 150 символов. Каков информационный вес каждого символа этого сообщения? 

2) В марафоне участвуют 12 спортсменов. Специальное устройство регистрирует прохождение финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого бегуна. Каков информационный объем сообщения, записанного устройством, после того как финиш пересекли 8 спортсменов?

Разбор задач можно найти на этой странице.

Задание 2.  Умение кодировать и декодировать информацию

Валя шиф­ру­ет рус­ские слова (по­сле­до­ва­тель­но­сти букв), за­пи­сы­вая вместо каж­дой буквы её код:

А	Д	К	Н	О	С
01	100	101	10	111	000

Не­ко­то­рые це­поч­ки можно рас­шиф­ро­вать не одним спо­со­бом. На­при­мер, 00010101 может озна­чать не толь­ко СКА, но и СНК. Даны три ко­до­вые це­поч­ки:

1010110

100000101

00011110001

Най­ди­те среди них ту, ко­то­рая имеет толь­ко одну рас­шиф­ров­ку, и за­пи­ши­те в от­ве­те рас­шиф­ро­ван­ное слово.

Решение.

Про­ана­ли­зи­ру­ем каж­дый ва­ри­ант от­ве­та:

1) «1010110» может озна­чать как «НКН» так и «КАН».

2) «100000101» может озна­чать как «ДСК» так и «НСАА».

3) «00011110001» может озна­чать толь­ко «СОДА».

Сле­до­ва­тель­но, ответ «СОДА».

Задание 3. Умение определять значение логического выражения.

Справка

Условные обозначения логических операций

¬ A,                             не A (отрицание, инверсия)

1. Ù B, A & B                A и B (логическое умножение, конъюнкция)
1. Ú B                          A или B (логическое сложение, дизъюнкция)

Приоритет логических операций (порядок выполнения):

1. отрицание НЕ, 2) умножение И, 3) сложение ИЛИ.

Таблицы истинностей

0 – ложь, 1 - истина А не А 0 1 1 0

А В А и В А или В 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 1

Закон де Моргана:

НЕ (А И В)= НЕ (А) ИЛИ НЕ (В)

НЕ (А ИЛИ В)= НЕ (А) И НЕ (В)

Пример

Для какого наибольшего значения числа Х истинно выражение  НЕ(X⩾56) И (X<14)?

Решение.

Сначала стоит убрать отрицание. Если X⩾56 - это все числа, которые больше или равны 56, то отрицание X⩾56 - это числа, меньшие (строго меньшие) 56:

Получатся, что наше число должно быть строго меньше 56 и X<14, значит еще и меньше 14. Поэтому получаем ответ 13.

Ответ: 13.

Пример

Напишите количество целых значений Х истинно выражение  НЕ((X⩽21) ИЛИ (X⩾84))?

Решение.

Сначала стоит убрать отрицание. По закону де Моргана (см. выше), получаем:

 НЕ (X⩽21) И  НЕ(X⩾84)

 НЕ (X⩽21) - это Х>21

НЕ(X⩾84) - это Х<84

Таким образом, получаем, что наши числа должны быть больше 21 и меньше 84, то есть 21<X<84. Таких чисел было 84-21-1=62. Минус 1 здесь из-за того, что числа 21 и 84 мы брать не должны. Проверку можно сделать так: сколько чисел между 8 и 10, если не учитывать эти числа? 10-8=2, но у нас должно получиться ровно одно число - 9, поэтому не забыть сделать 2-1=1.

Ответ 62.

Задание 4. Умение анализировать формальные описания реальных объектов и процессов.

Между населёнными пунктами A, B, C, D, E, F построены дороги,
протяжённость которых (в километрах) приведена в таблице.

	A	B	C	D	E	F
A		3	5			15
B	3		3
C	5	3		5	2
D			5			3
E			2			7
F	15			3	7

Определите длину кратчайшего пути между пунктами A и F. Передвигаться
можно только по дорогам, указанным в таблице.

Решение 

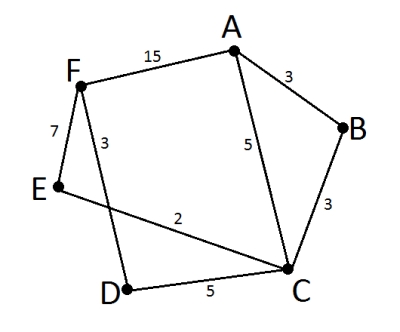
Для удобства отобразим табличные данные в виде графа

Теперь переберем все возможные пути из A в F:

A-B-C-E-F = 3+3+2+7 = 15

A-B-C-D-F = 3+3+5+3 = 14

A-C-E-F = 5+2+7 = 14

A-C-D-F = 5+5+3 = 13

ну и A-F = 15

Как видно, кратчайший вариант A-C-D-F = 13км. Правильный ответ 13.

Чтобы не запутаться, рекомендуется перебирать пункты в алфавитном порядке.

Задание 5.  Умение  исполнить  алгоритм для  конкретного  исполнителя с  фиксированным  набором команд

Пример

У исполнителя Информашка две команды, которым присвоены номера:
1. прибавь 2
2. умножь на х (х – неизвестное натуральное число; х ≥ 2)
Выполняя первую из них, Информашка увеличивает число на экране на 2, а выполняя вторую, умножает это число на х .
Программа для исполнителя Информашка – это последовательность номеров команд.
Известно, что программа 11211 переводит число 3 в число 74. Определите значение х.

Решение

Можно построить последовательность действий:

1) первая команда +2, поэтому: 3+2=5

2) вторая команда тоже +2, поэтому 5+2=7

3) затем надо умножить число из 2го шага умножить на х, поэтому: 7*х

4) к числу, полученному на 3 шаге надо прибавить +2: 7*х+2

5) и, наконец, к 4му шагу прибавляем опять 2: 7*х+2+2

По условию получается, что после последнего шага получили число 74, поэтому:

7*х+2+2=74

Осталось найти х:

7*х+4=74

7*х=74-4

7*х=70

х=70/7

х=10

Ответ 10

Пример задания. Старая версия

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след  в  виде  линии.  Чертёжник  может  выполнять  команду Сместиться на (a, b) (где a, b – целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Если числа  a,  b  положительные,  значение  соответствующей  координаты
увеличивается, если отрицательные – уменьшается.

Например,  если  Чертёжник  находится  в  точке  с  координатами (4, 2),  то команда Сместиться на (2, –3) переместит Чертёжника в точку (6, –1).
Запись
Повтори k раз
Команда1 Команда2 Команда3
Конец
означает,  что  последовательность  команд  Команда1  Команда2  Команда3 повторится k раз.

Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 раз
Сместиться на (–2, –1) Сместиться на (3, 2) Сместиться на (2, 1)
Конец

На  какую  одну  команду  можно  заменить  этот  алгоритм,  чтобы  Чертёжник оказался в той же точке, что и после выполнения алгоритма?

1) Сместиться на (–9, –6)

2) Сместиться на (6, 9)

3) Сместиться на (–6, –9)

4) Сместиться на (9, 6)

Решение:

Чтобы решать такие задания проще всего составить уравнения. Чтобы найти точку по оси х, в которой оказался исполнитель, необходимо сложить все координаты по х(не забыть умножить на число повторов), аналогично по оси у. По оси х получим:

(-2+3+2)*3=х => x=9

(-1+2+1)*3=у => y=6

Таким образом, ответ 4) Сместиться на (9, 6)

Задание 6. Анализ программного кода

Ниже приведены программа

s=int(input())

k=int(input())

if s>8 and k<=4:

    print ("ДА")

else:

    print ("НЕТ")

Было проведено 9 запусков программы, при которых в качестве значений переменных s и k вводились следующие пары чисел: (10, 8); (12,4); (-6,-6); (8,3); (15,-15); (11, -5); (10,0); (2, 10); (10, 10). Сколько было запусков, при которых программа напечатала «ДА»?

Решение

Рассмотрим конструкцию if s>8 and k<=4

Логическая связка and - означает, что должны выполниться одновременно оба условия и первое, s>8, и второе k<=4. То есть нам подойдут такие пары, где первое число строго больше 8, а второе меньше или равно 4:
(10, 8) нет подходит, второе число не меньше либо равно 4 (8<=4 - это ложь)

 (12,4) подходит: первое больше 8, а второе равно 4

(-6,-6) нет подходит: первое число не больше 8

(8,3) нет подходит: первое число не больше 8

(15,-15) подходит: первое больше 8, а второе меньше 4

(11, -5)  подходит: первое больше 8, а второе меньше 4

(10,0) подходит: первое больше 8, а второе меньше 4 

(2, 10) нет подходит: первое число не больше 8

(10, 10) нет подходит: второе число не меньше 4.

Пар чисел, которые нам подойдут получилось 4.

Ответ 4

Задание 7. Умение использовать информационно-коммуникационные технологии. 

Для решения достаточно знать как формируется адрес в Интернет. Сначала идет протокол (как правило это ftp или http), потом ://, потом сервер, затем /, а в конце файл:

протокол://сервер/файл

или кратко ПСФ

Пример:

Доступ  к  файлу  hello.jpg,  находящемуся  на  сервере  home.info, осуществляется  по  протоколу  ftp. Фрагменты  адреса  файла  закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

А) info

Б) ://

В) home.

Г) /

Д) hello

Е) ftp

Ж) .jpg

Получаем: ЕБВАГДЖ

Задание 8. Умение осуществлять поиск информации в Интернете

Если у нас есть запрос А и запрос В, то  А | В можно показать на схеме:

Как видно из схемы, нам подойдут и те страницы в интернет, где есть только одно слова А, и те, где есть только слово В, а также те, где встречаются оба слова вместе. Но если мы просто сложим количество страниц со словом А и количество страниц со словом И, то мы два раза посчитаем из пересечение - & (на схеме видно, что место пересечения закрашено два раза). Поэтому надо вычесть из суммы это пересечение. Получим формулу:

A+B-А&B=A|B

Пример

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов

Запрос	Найдено страниц (в тысячах)
ОГЭ& ЕГЭ	490
ОГЭ	680
ЕГЭ	890

Какое количество страниц (в тысячах) будет найдено по запросу ОГЭ | ЕГЭ?

Решение

По формуле получаем:

ОГЭ + ЕГЭ - ОГЭ & ЕГЭ=ОГЭ | ЕГЭ

Подставим числа: 

680+890-490=1080

Ответ 1080

Задание 9. Умение анализировать информацию, представленную в виде схем

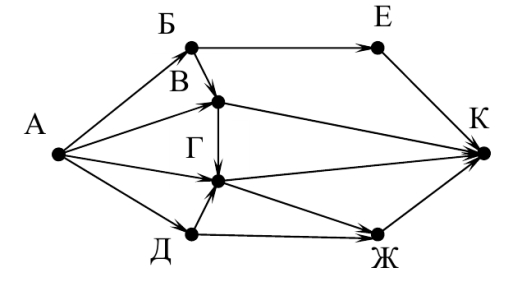
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой  дороге  можно  двигаться  только  в  одном  направлении,  указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Г?

Решение

Сначала уберем те пути, которые не идут через город Г:

Теперь подсчитаем количество дорог ведущих в каждую вершину, из А в Б ведет одна дорога, а вот из В ведет одна дорога из А и одна из Б, получается 2:

Аналогично подсчитаем дороги, ведущие в Г: из А в Д ведет одна дорога, и из Д в Г тоже 1, Из а в Г тоже 1 дорога, а из В 2 дороги, получается 1+1+2=4:

Досчитываем до конца:

Ответ 8.

Второй способ

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой  дороге  можно  двигаться  только  в  одном  направлении,  указанном стрелкой. Сколько существует различных путей из города А в город К?

Данный тип задач нацелен на проверку умения  анализировать  информацию, представленную в виде схем. При решении есть вероятность запутаться в большом количестве вариантов.

Итак, начнем решение с конца, т. е. с города К. Как мы видим, в город К можно приехать из городов Е, В, Г, Ж. Отобразим это графически

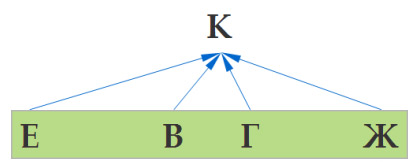
Задача 11 ГИА по информатике. Шаг 1

Далее, на втором шаге определим, откуда можно добраться в города Е, В, Г, Ж. К примеру,

• в город Е можно добраться только из города Б,
• в город В — из городов А и Б,
• в город Г из городов А, В и Д,
• в город Ж из городов Г и Д.

Таким образом, мы будем продолжать до тех пор, пока каждая ветка не приведет к городу А. В итоге получится такая диаграмма — дерево:

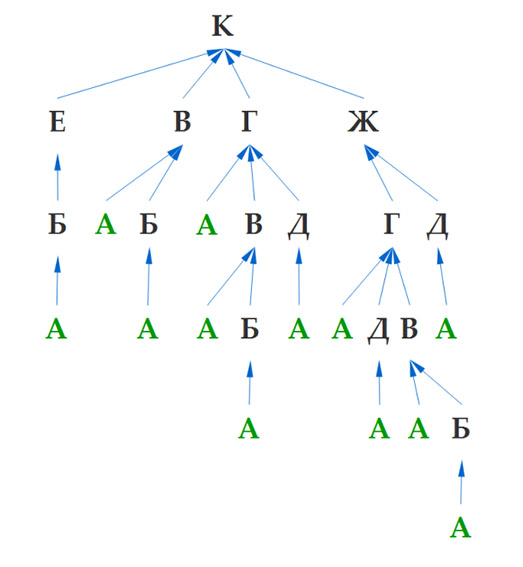
Здесь зеленым цветом я выделил конечные пункты — город А. Осталось только посчитать их количество — это и будет правильный ответ. В нашем случае их 12. Правильный ответ: 12.

Задание 10. Системы счисления

Правила перевода в десятичную систему счисления.

Каждую цифру числа умножаем на основание системы счисления в степени от 0 до n.

Разбор:

Под каждой цифрой числа напишем, начиная с 0, порядковые номера. Начнем с самого младшего разряда - единиц:

123₈
^{2 1 0}

Затем каждую цифру числа умножаем на основание системы счисление ( у нас - 8) в степени, что подписана под цифрой:

Осталось подсчитать. Помним, что любое число в 0 степени равно 1, n⁰=1:

123₈= 3*8⁰+2*8¹+1*8²=3+16+64=83₁₀

Аналогично переводится остальные системы счисления.

Про шестнадцатеричную систему не забываем, что:

А=10

B=11

C=12

D=13

E=14

F=15

Пример 

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

26₁₆,43₈,11101₂

Решение

26₁₆=6*16⁰+2*16¹=6+32=38₁₀

43₈=3*8⁰+4*8¹=3+32=35₁₀

11101₂=1*2⁰+0*2¹+1*2²+1*2³+1*2⁴=1+4+8+16=29₁₀

Ответ 38